Tarjan's Algorithm: Finding Strongly Connected Components

Introduction

Graphs are widely used to model real-world systems such as social networks, communication channels, and dependency structures. In directed graphs, cycles are particularly significant, and analyzing them through Strongly Connected Components (SCCs) provides valuable insight into the graph’s structure.

An SCC is defined as a subset of nodes in which every node is reachable from every other node within the same subset. Identifying these components is important in applications like deadlock detection, dependency analysis, and compiler optimization.

Among the most efficient methods for this task is Tarjan’s Algorithm, which leverages Depth-First Search (DFS) along with discovery and low-link values to compute SCCs in linear time. This article explains the concept of SCCs and illustrates Tarjan’s Algorithm step by step with examples.

But before diving right into the algorithm, here’s a brief recap of the associated concepts.

Graph

A graph is a mathematical structure, particularly in graph theory, consisting of vertices(nodes) and edges that interlink the nodes with each other. In the context of computer science, however, a graph refers to a data structure whose vertices represent some kind of entity(it may be a network node or some data) that is linked to other vertices using connection links(edges).

It consists of two sets: \(\mathbf{V} = \{ v \;|\; \text{set of all vertices} \}\) \(\mathbf{E} = \{ e \; |\; \text{set of all the edges}\}\)

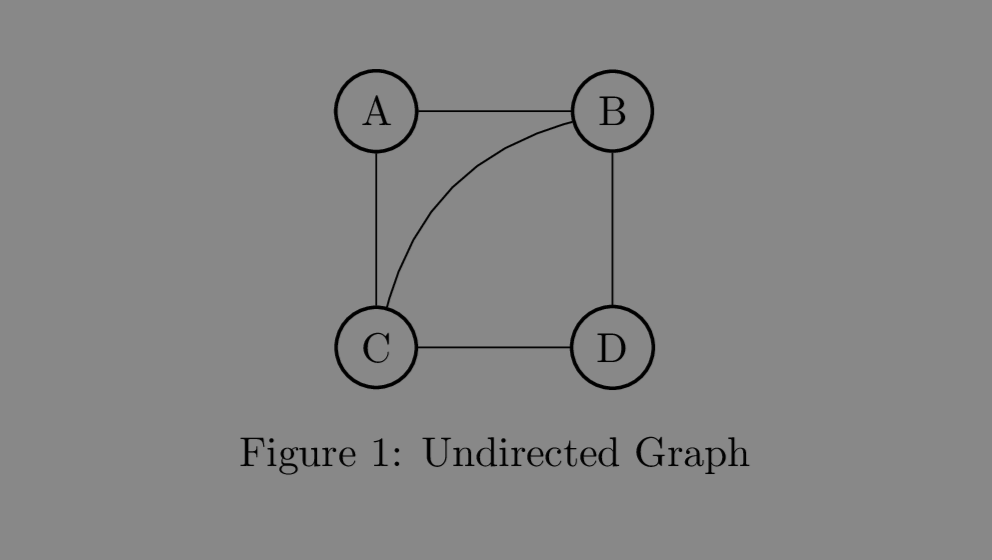
Pictorially, it is depicted as circles connected by lines or arrows for different types of graphs.

Two nodes are said to be adjacent if they have an interconnecting edge between them. Adjacency simplifies the concept of interconnection by considering only the nodes adjacent to a given node. Given the above graph, we see that the adjacency list of node A is: $[\text{B}, \; \text{C}]$. This simplification is important for computers to work with graphs.

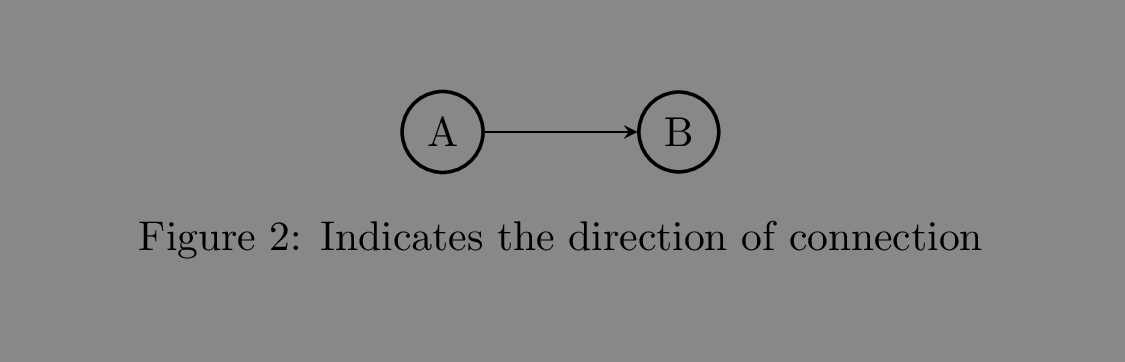
Furthermore, edges can be directed or undirected. A directed edge represents a unidirectional connection between the two nodes wherein we can only move from one node to the other but not in the other direction, and is commonly depicted with a pointed arrow where the arrowhead represents the node that can be reached from the node at the base.

An undirected edge, on the other hand, represents a bidirectional connection between the two nodes.

Based on the nature of the edges between the nodes of a graph, there are two types of graphs that are commonly used in computer science: undirected graphs and directed graphs.

Now, that we have a basic overview of a graph, let’s delve into the problem that this algorithm attempts to solve and the important concepts behind this algorithm.

Strongly Connected Components

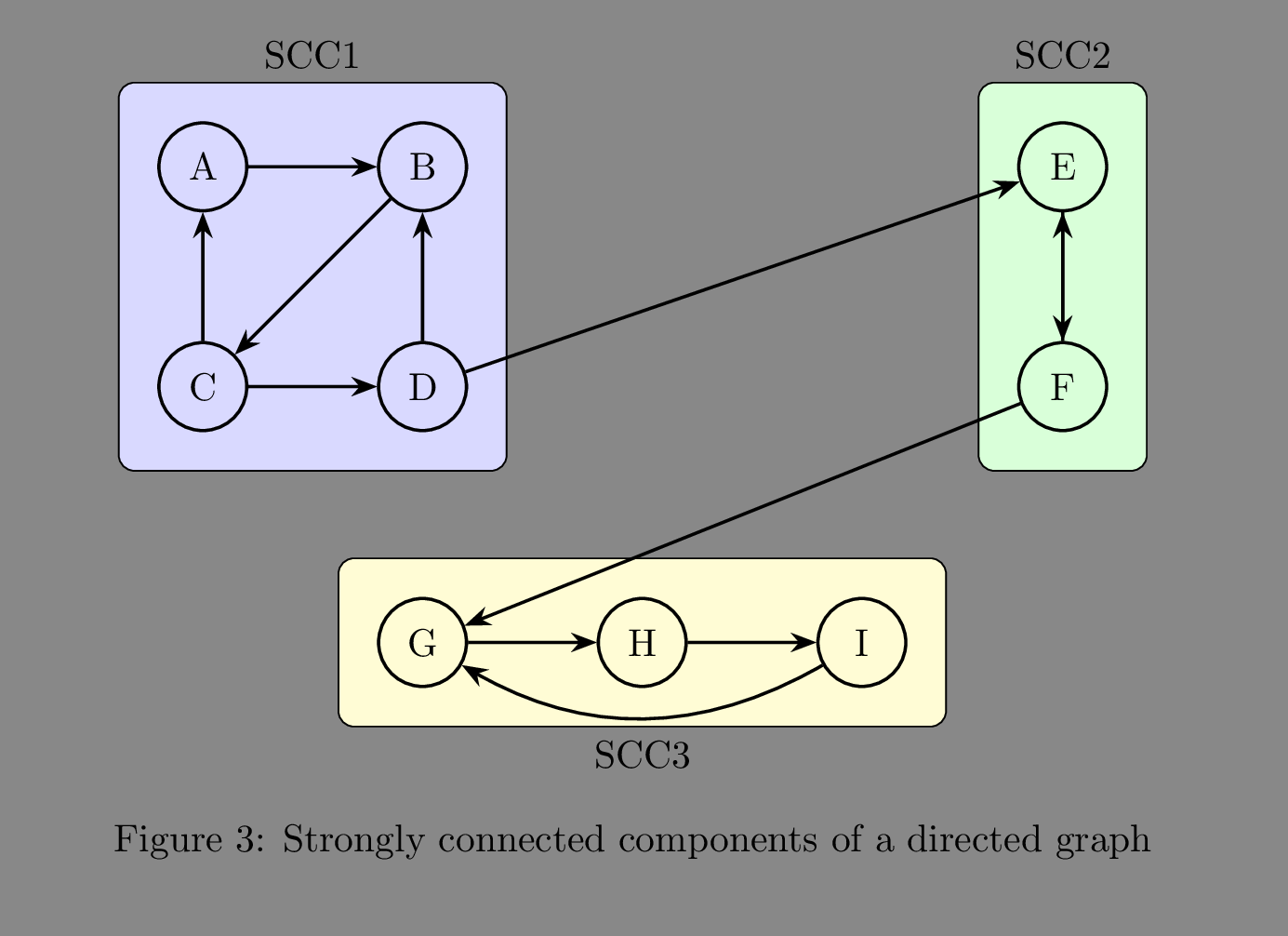
A strongly connected component of an directed graph is a maximal subgraph where each vertex(node) is mutually reachable, meaning starting at any arbitrary node in the graph, we can get to any other vertex in the subgraph.

A subgraph refers to a portion of a graph, or more formally, a subset of the vertex set that is obtained by removing some vertices(nodes) from it and all the edges incident to those vertices. Whereas the maximality condition refers to the fact that the subgraph can not be extended by adding a vertex from the original graph whilst maintaining the mutual reachability condition. The strongly connected components, therefore, partitions the graph into disjoint subgraphs.

Depth-first Search

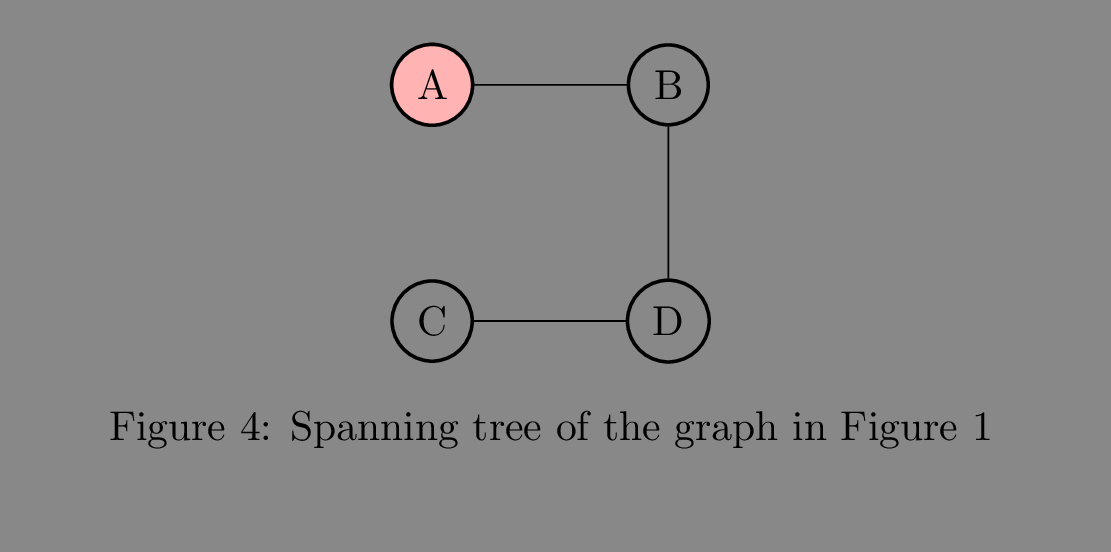
Depth-first Search is a traversal algorithm that traverses the graph recursively, by first exploring one of the adjacent nodes of the passed node and then backtracking to the original node and exploring any other adjacent node that it may have. The important thing to note is that it traverses the graph as a spanning tree. A spanning tree of a connected graph(connected means that there are no isolated subgraphs) connects all the nodes of the graph using the minimum number of edges and contains no cycles. And since there are many spanning trees of a graph, the DFS traversal order is not unique.
Considering the graph in figure 1 and starting at A, one possible spanning tree is:

But, during the traversal, we need to keep track of already visited nodes to prevent indefinite behavior because of the presence of cycles, which can be achieved by using an array.

Some additional concepts

As stated above, the DFS traverses the graph as a spanning tree; such a spanning tree has two kinds of edges: tree edges and back edges. Back edges relate a tree node to its ancestor in the traversal order, whereas a Tree edge takes us from the parent node to its children when the graph is traversed as a spanning tree.

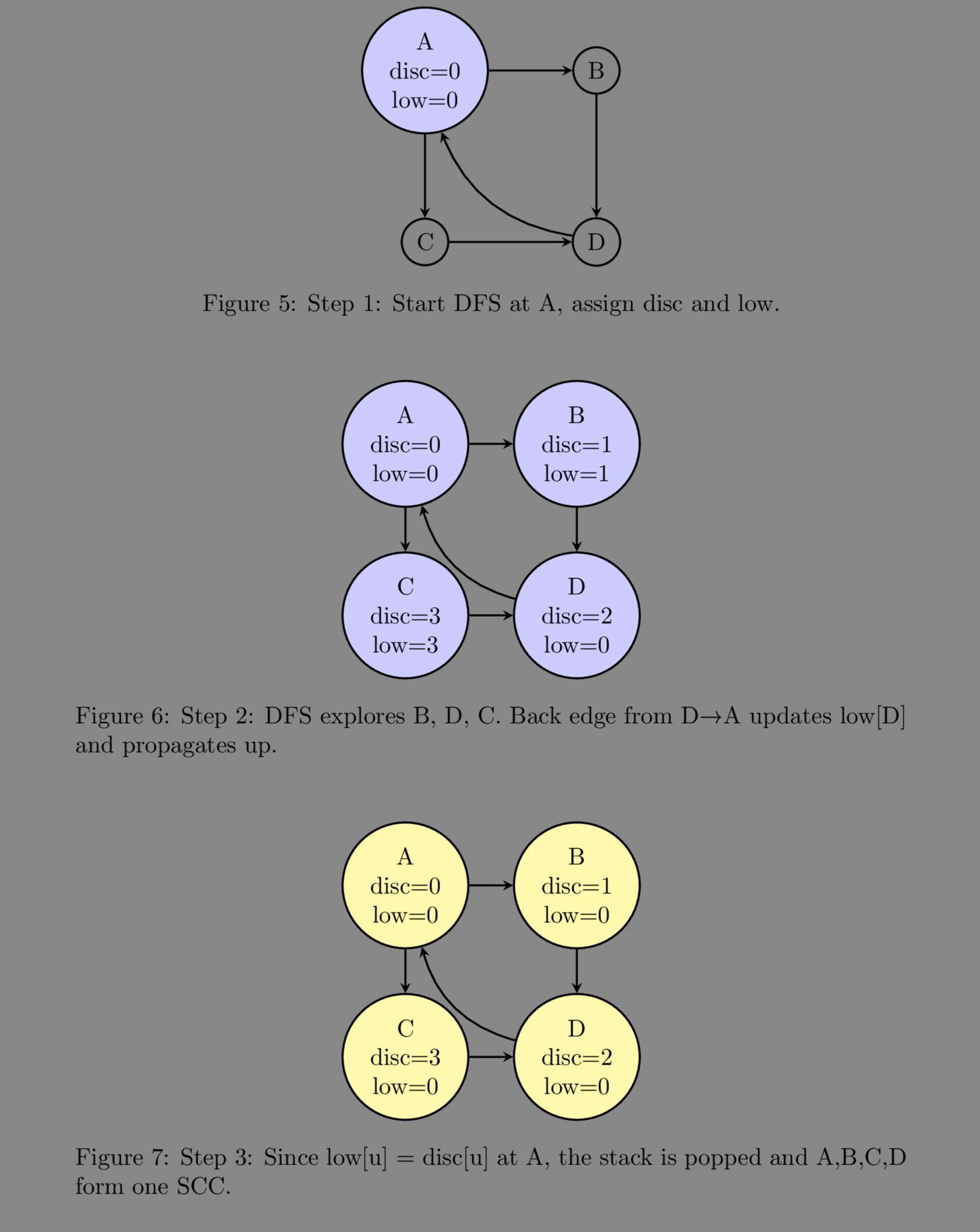
However, the two most important concepts responsible for this algorithm’s efficiency are discovery time and low values. Discovery time is the time it takes for the DFS to reach a node in its traversal. Conventionally, the time starts from 0, and the first node is assigned 0 as its discovery time, and it is incremented as the algorithm goes from a node to its adjacent node. On the other hand, Low values indicate the node with the smallest discovery time that can be visited from the given node. Low values less than a node’s discovery time indicate a backedge from the node or its descendants to its ancestor(a cycle).

Tarjan’s algorithm for directed graphs

Tarjan’s algorithm is used to find the Strongly Connected Components(SCCs) of a directed graph.

Algorithm

• We start off at any vertex and assign it a discovery time and a low value of 0.
• Then, we iterate over its adjacent nodes, and for the unvisited nodes(at this point, all the adjacent nodes will be unvisited), we recursively call the DFS routine.
• For each subsequent node, we assign it a discovery time and a low value and push it onto a stack, and then iterate over its adjacent nodes and do the following steps
  • If the adjacent node has already been visited, which indicates a back edge and hence, a cycle, we update the current node’s(u) low value as $low[u] = min(low[u], \; disc[v])$.
  • If the adjacent node has not been visited yet, we call the DFS routine for that node and on backtracking, update the current node’s low value as $low[u] = min(low[u], \; low[v])$. This is necessary to propagate the low value of the descendants up to u.
• SCC identification: If $low[u] = disc[u]$, then u is the root of a strongly connected component and we pop the nodes from the stack until u is popped, indicating that the SCC with u as its root has been removed and we repeat the process.

Tarjan’s algorithm for undirected graphs

A slightly modified version of Tarjan’s algorithm is used for undirected graphs to find the bridges and articulation points in the graph. Bridges are the edges whose removal increases the number of connected components of the graph, whereas articulation points are the vertices(nodes) whose removal increases the number of connected components.

Algorithm

• We start off at any vertex and assign it a discovery time and a low value of 0.
• Then, we iterate over its adjacent nodes, and for the unvisited nodes(at this point, all the adjacent nodes will be unvisited), we recursively call the DFS routine with the current node as the parent node.
• For each subsequent node, we assign it a discovery time and a low value, and then iterate over its adjacent nodes and do the following steps
  • If the adjacent node is the parent of the current node in the DFS traversal order, we skip it.
  • If the adjacent node has already been visited, which indicates a back edge and hence, a cycle, we update the current node’s(u) low value as $low[u] = min(low[u], \; disc[v])$.
  • If the adjacent node has not been visited yet, we call the DFS routine for that node with the current node as its parent, and on backtracking, update the current node’s low value as $low[u] = min(low[u], \; low[v])$. This is necessary to propagate the low value of the descendants up to u.
• Check for Bridges: If $low[u] > disc[v]$, then $(u, v)$ is a bridge because it means that all paths from v to an ancestor of u go through $(u, v)$.
• Check for Articulation Points: If $disc[u] \leq low[v]$, then u is an articulation point unless it is the root of the spanning tree, because it means that no descendant of u can go to an ancestor of u without passing through u.

Note: In the case of undirected graphs, we skip the parent node because every such edge, that is, between a parent and its child, can be considered a bridge unless there’s a back edge between the child and an ancestor of the parent, which we are interested in finding.

Conclusion

For undirected graphs, Tarjan’s algorithm can be effectively used to find bridges and articulation points, which are crucial for understanding the connectivity and structure of the graph. By modifying the DFS traversal to account for back edges and parent-child relationships, we can identify these critical components and gain insights into the graph’s topology.

References

1. R. E. Tarjan. Depth-first search and linear graph algorithms. SIAM Journal on Computing, 1(2), 146–160, 1972. doi:10.1137/0201010.
2. T. H. Cormen, C. E. Leiserson, R. L. Rivest, and C. Stein. Introduction to Algorithms, 3rd Edition. MIT Press, 2009.
3. GeeksforGeeks. Tarjan’s Algorithm to Find Strongly Connected Components. https://www.geeksforgeeks.org/tarjan-algorithm-find-strongly-connected-components/. Accessed: Aug 2025.